Pada artikel ini kita akan membahas materi tentang pertidaksamaan dan interval untuk lebih jelasnya akan saya jelaskan di penjelasan dibawah ini :
Pengertian pertidaksamaan
pertidaksamaan adalah himpunan bilangan yang memenuhi sifat urutan bilangan tertentu. Pertidaksamaan dinyatakan dengan salah satu tanda dari lambang berikut = (<,>,
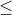
,
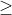
,).
a. x < y yang menyatakan bahwa nilai x lebih kecil dari nilai y.
b. x > y yang menyatakan bahwa nilai x lebih besar dari nilai y.
c. x
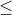
y yang menyatakan bahwa nilai x lebih kecil atau sama dengan nilai y.
d. x
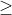
y yang menyatakan bahwa nilai x lebih besar atau sama dengan nilai y.
Sifat - sifat operasi sederhana :
1. Penjumlahan
jika x > y maka x + a > y + a, kita misalkan x = 2, y = 1, a = 3, kita masukkan nilai tersebut kedalam x + a > y + a = 2 + 3 > 1 + 3 = 5 > 4 .
2. Pengurangan
Jika x < y maka x - a < y - a, kita misalkan x = 1, y=2,a=3,kita masukkan nilai tersebut kedalam x -a <y- a = 1- 3 < 2-3= -2 < -1.
3. Perkalian
Jika x
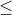
y maka ax
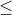
ay, kita misalkan x = 1,y=1,a=3, kita masukkan nilai tersebut kedalam ax
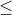
ay = 1(3)
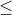
1(3) = 3
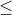
3 .
4. Pembagian
Jika x
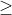
y maka

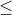

kita misalkan x = 1,y = 1,a=3, kita masukkan nilai tersebut kedalam

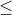

=

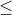

.
Pertidaksamaan dan interval
a. Jika

= 0 solusinya adalah sebuah titik didalam garis bilangan R (x1 = (-5),x2 = 2).
b. Jika

bertanda (<,>,
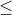
,
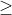
,) maka solusinya berupa garis bilangan yang tertutup ataupun terbuka.
Pertidaksamaan kuadratik
Merupakan pertidaksamaan yang memuat persamaan kuadrat didalamnya.
Contoh =

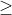
0
Cara mencari solusi dari persamaan kuadratik adalah dengan mencari akar - akar dari persamaan tersebut dengan menfaktorkanya agar mendapatkan akar - akar dan setelah itu membuat garis bilangan agar dapat mengetahui himpunan solusi dari pertidaksamaan kuadratik tersebut.
Pertidaksamaan bentuk pecahan
Pertidaksamaan dalam bentuk pecahan memiliki sifat - sifat sebagai berikut :
1. Jika

> 0 maka

harus bernilai positif dengan x dan y keduanya harus benilai positif ataupun keduanya bernilai negatif.
2. Jika

< 0 maka

harus bernilai negatif dengan x dan y dari salah satu keduannya ada yang bernilai negatif.
Himpunan penyelesaian dan garis bilangan
a. Jika pertidaksamaan memiliki tanda < atau > maka dibuat bulatan pada akar - akar yang didapat pada garis bilangan tetapi bulatan tersebut tidak harus dihitamkan.
b. Jika pertidaksamaan memiliki tanda
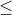
ataupun
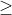
maka dibuat bulatan pada akar -akar yang didapat pada garis bilangan dengan menghitamkan bulatan tersebut.
untuk lebih jelasnya bisa dilihat gambar dibawah ini :
Sumber gambar :
Contoh soal dan pembahasan
1.diberika pertidaksamaan sebagai berikut :
Penyelesainya :
Karena pertidaksamaan diatas tidak bisa difaktorkan maka kita menggunakan rumus abc untuk mencari faktor - faktor dari persamaan tersebut.
Dengan a = 3,b = 1 dan c = (-4), maka kita masukan nilai abc kedalam rumus diatas.

Dan garis bilanganya adalah sebagai berikut :
Karena tanda pada pertidaksamaan adalah
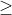
maka bulatan pada garis bilangan dihitamkan dan himpunan penyelesainya berada pada titik + jadi himpunan solusi dari pertidaksamaan diatas adalah
2. Diberikan pertidaksamaan sebagai berikut :
Penyelesainya :
Karena penyebut tidak bisa difaktorkan kita hanya perlu mencari nilai dari diskriminanya untuk mewakili dari nilai penyebut dari pertidaksamaan diatas.
Kita masukkan nilai dari persamaan penyebutnya sebagai berikut :
D < 0 dan a > 0 maka definit positif tidak memiliki akar real oleh karena itu nilai akar dari penyebut tidak dapat dimasukkan kedalam pembuat nol.
Kita buat pembuat nol :
x - 3
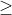
0
x
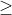
3
Kita buat garis bilangan :
Himpunan solusi dari pertidaksamaan diatas adalah x
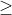
3.
Demikianlah penjelasan saya mengenai pertidaksamaan dan garis bilangan lebih dan kurangnya mohon dimaafkan jika ada saran dan komentar silakan dimasukkan di dalam kolom di bawah ini.


































